Comprender la diferencia: exactitud frente a precisión

La exactitud y la precisión tienen significados distintos en el ámbito de las mediciones y el análisis de datos. La precisión se refiere a la proximidad de una medición o serie de puntos de datos al valor real; cuanto menor sea el error de observación, mayor será la precisión. Este concepto está relacionado con el sesgo y el error sistemático, ya que estos factores pueden sesgar significativamente la precisión de la cifra.

La precisión, por otro lado, se refiere a la reproducibilidad o repetibilidad de las mediciones. Refleja la variabilidad estadística dentro de una muestra estadística. Una mayor precisión implica menos errores aleatorios y una mayor resolución de medición. 

Comprender la diferencia entre estos dos conceptos es esencial para la aplicación del método científico y el análisis numérico.

Introducción a la exactitud y la precisión

La exactitud y la precisión son muy importantes cuando se hace ciencia. Se refieren a cuán cerca están tus mediciones de lo que realmente estás tratando de medir. La exactitud es dar en el blanco, mientras que la precisión es dar en el mismo punto una y otra vez. Ambos se ven afectados por factores como errores en la forma de medir o simplemente por el azar.

Para confiar en tus números, tienes que garantizar la exactitud y la precisión. Si no lo haces, incluso un pequeño error o un poco de mala suerte pueden echar por tierra todo tu experimento. Por eso los científicos trabajan duro para asegurarse de hacerlo bien.

Definición de precisión

Obtener una medición correcta significa que es precisa. Lo importante es estar a la altura, incluso si hay cosas como errores aleatorios o problemas más graves que afectan a tus resultados. La precisión es muy importante en la ciencia: es lo que hace que un experimento merezca la pena repetirse.

Cuando tus números varían demasiado, eso es variabilidad, y puede hacer que tus mediciones sean menos precisas. El sesgo o la imposibilidad de realizar mediciones muy precisas también pueden ser un problema. Todo esto puede hacer que tus datos pierdan precisión y afectar a tu experimento.

Definición de precisión

La precisión se basa en la consistencia. Es cuando tus mediciones se mantienen muy próximas entre sí, aunque no sean exactas. La precisión no se preocupa por las confusiones aleatorias o si te inclinas hacia un lado u otro, solo se trata de que los números sean similares.

Ser preciso es clave para una buena ciencia. Te ayuda a hacer lo mismo una y otra vez sin cometer errores. Es muy importante para garantizar que tus resultados sean fiables y mantener la solidez científica.

La importancia de la exactitud y la precisión en el análisis de datos

En el análisis de datos, es fundamental hacer las cosas bien y ser coherente. La precisión significa que puedes confiar en que los resultados serán siempre los mismos. La precisión se refiere a cuán cerca está tu medición de la realidad. Si no eres preciso, es posible que cometas errores constantes o que simplemente no alcances el objetivo, y si no eres exacto, tus resultados serán muy dispares.

Además, la fiabilidad de los datos depende de factores como el sesgo.

Para alcanzar realmente tus objetivos, debes reducir los errores y asegurarte de obtener los mismos resultados cada vez. Seguir el método científico es de gran ayuda para alcanzar estos objetivos.

El papel de la precisión en el análisis de datos

La precisión es muy importante en el análisis de datos porque te indica si puedes confiar en lo que estás viendo. Se trata de cuán cerca están tus números de la realidad, lo que te ayuda a evitar conjeturas erróneas. Cuando eres realmente preciso, no solo estás acertando en tus predicciones, sino que también te aseguras de que tus resultados sean fiables una y otra vez.

Además, ser preciso significa que tus datos son más fiables.

Cuando tus mediciones son consistentes, tus cálculos numéricos son precisos y es menos probable que te desanimes por los errores. Por lo tanto, la precisión no es solo algo deseable, sino imprescindible en la ciencia de resolver problemas con datos.

El papel de la precisión en el análisis de datos

La precisión es muy importante en el análisis de datos porque garantiza que tus mediciones sean fiables una y otra vez, reduciendo las conjeturas. En realidad, se trata de lo cerca que están entre sí tus intentos repetidos, lo que significa que hay menos posibilidades de que se produzcan confusiones aleatorias. Obtener la precisión adecuada es muy importante para garantizar que tus respuestas finales sean correctas.

Y la precisión hace que tus datos sean más sólidos al eliminar los errores recurrentes.

También significa que es menos probable que te dejes influir por cosas que podrían afectar tus resultados. Al formar parte del método científico, la precisión demuestra lo bueno que es tu juego de números y lo mucho que puedes confiar en tus datos.

Comprender la diferencia entre exactitud y precisión

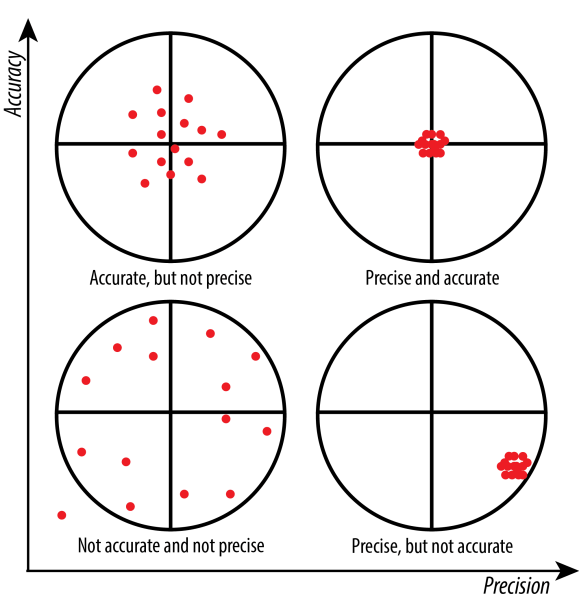
La exactitud se refiere a la proximidad de una medición al valor real, mientras que la precisión se refiere a la repetibilidad o reproducibilidad de las mediciones. Por ejemplo, si varios puntos de datos tomados de una muestra estadística se encuentran muy próximos entre sí, esto indica una alta precisión, pero estos resultados podrían estar lejos del valor real debido a un sesgo o un error sistemático.

Por otro lado, las mediciones que son exactas pero no precisas pueden indicar un alto error de observación, errores aleatorios o varianza causada por la variabilidad estadística. El método científico exige tanto exactitud como precisión para minimizar el sesgo y la variabilidad, y para evaluar eficazmente la resolución de las mediciones o el análisis numérico.

Comparación entre exactitud y precisión

La exactitud y la precisión son dos factores cruciales en los estudios científicos que se ocupan de las mediciones. La precisión se refiere a la proximidad de los puntos de datos de la muestra estadística al valor real, donde un menor error de observación indica una mayor precisión. Por otro lado, la precisión se refiere a la repetibilidad y reproducibilidad de las mediciones, que depende de la densidad con la que se agrupan los puntos de datos.

Sin embargo, las mediciones precisas pueden seguir teniendo problemas de precisión en casos de alta variabilidad estadística o errores aleatorios. Además, la precisión también podría verse afectada por la resolución de la medición. Por el contrario, las mediciones precisas podrían no ser exactas si existe un sesgo o error sistemático.

Ejemplos que ilustran la diferencia

Al realizar un análisis numérico, un científico aplica el método científico para recopilar e interpretar puntos de datos. Sin embargo, este enfoque no es inmune a los errores de observación. Este error puede producirse como errores aleatorios, introducidos por la variabilidad estadística en el proceso de medición, o como errores sistemáticos, una desviación constante del valor real, a menudo debido a un sesgo en la recopilación o a problemas de resolución de la medición.

Por lo tanto, la precisión de las mediciones se ve afectada por ambos tipos de errores. Los errores aleatorios contribuyen a la variabilidad de los resultados, por lo que el mismo experimento, si se repite, podría no producir el mismo resultado, lo que afecta a la reproducibilidad. Los errores sistemáticos, a su vez, perjudican la repetibilidad, ya que el mismo método defectuoso producirá continuamente resultados igualmente erróneos.

Por lo tanto, es esencial contar con una muestra estadística sólida para mitigar estos problemas y obtener resultados fiables.

Cómo la exactitud y la precisión influyen en las decisiones empresariales

La exactitud y la precisión son aspectos importantes que a menudo influyen en las decisiones empresariales. Determinan la fiabilidad de los datos y la información utilizados en el proceso de toma de decisiones. La exactitud se refiere a la proximidad de una medición al valor real, mientras que la precisión se refiere a la repetibilidad o reproducibilidad de las mediciones. Una mayor precisión reduce el error de observación.

La imprecisión suele deberse a errores aleatorios y a la variabilidad estadística entre los puntos de datos, mientras que la inexactitud puede deberse a errores sistemáticos o sesgos. Una medición inexacta o una encuesta con una muestra estadística significativamente variable puede dar lugar a decisiones empresariales perjudiciales. El análisis numérico ayuda a optimizar la precisión y minimizar el sesgo, lo que reduce los errores y conduce a una mejor toma de decisiones.

Efecto de la precisión en las estrategias empresariales

La precisión en las mediciones, los errores aleatorios y los errores de observación influyen significativamente en las estrategias empresariales. Si la muestra estadística no representa adecuadamente la variabilidad de los puntos de datos, puede dar lugar a decisiones sesgadas, lo que afectaría a la reproducibilidad de un modelo de negocio.

La precisión también afecta a la repetibilidad y la resolución de la medición, que son esenciales para evaluar el rendimiento de diversas estrategias. Un error sistemático puede distorsionar el valor real obtenido del análisis numérico, lo que puede conducir a decisiones estratégicas erróneas. Además, ignorar la variabilidad estadística puede conducir a la violación del método científico en los procesos de toma de decisiones.

Efecto de la precisión en las estrategias empresariales

Las estrategias empresariales se benefician enormemente de la precisión en el análisis y la medición de datos. Las mediciones precisas minimizan los errores de observación y mitigan los sesgos, lo que ayuda a proporcionar una imagen más clara del valor real de las métricas empresariales. Además, el método científico puede mejorar significativamente la repetibilidad y reproducibilidad de los resultados, proporcionando una muestra estadística más fiable con la que trabajar.

Sin embargo, es fundamental recordar que incluso las mediciones más precisas pueden contener errores aleatorios o sufrir variabilidad estadística. Por lo tanto, las empresas deben interpretar los datos de forma sensata, teniendo en cuenta los posibles errores sistemáticos y los límites inherentes a la resolución de las mediciones.

Solución esencial para la gestión de proyectos

Bonsai es el software definitivo para la colaboración en proyectos, diseñado para unir a los equipos y optimizar todos los aspectos de la gestión de proyectos. Bonsai incorpora varias soluciones esenciales de gestión de proyectos que son fundamentales para completar con éxito los proyectos. La implementación de controles de proyectos es otra técnica que facilita Bonsai.

‍

Ayuda a supervisar el progreso del proyecto y a realizar los ajustes necesarios para mantenerlo en marcha. Al utilizar estas técnicas en Bonsai, los gestores de proyectos pueden garantizar que todos los aspectos del proyecto estén bien planificados, se ejecuten de manera eficiente y se completen con éxito.

Herramientas para medir la exactitud y la precisión

La exactitud y precisión de las mediciones científicas se evalúan normalmente mediante herramientas como el análisis numérico, que mide la proximidad de las mediciones al valor real. Este proceso implica tener en cuenta los errores sistemáticos, los errores aleatorios y los errores de observación. Estos son factores cruciales para reducir el sesgo y mejorar la resolución de la medición.

Otra herramienta integral es la evaluación de la variabilidad, que incluye la variabilidad estadística. Esto se hace analizando el rango de puntos de datos en una muestra estadística. Un aspecto importante de este proceso es garantizar la repetibilidad y reproducibilidad de las mediciones.

Por último, el método científico también sirve como herramienta para medir la exactitud y la precisión, guiando la recopilación e interpretación de las mediciones. Esto ayuda a mitigar problemas como el sesgo y corrobora aún más la fiabilidad de los resultados.

Microsoft Excel para mediciones precisas y exactas.

Microsoft Excel ofrece varias herramientas para gestionar y analizar mediciones de exactitud y precisión en el análisis de datos, lo que reduce significativamente el error de observación. Es especialmente útil cuando se trabaja con una muestra estadística grande, ya que proporciona una plataforma para realizar análisis numéricos detallados. Excel ayuda a identificar y gestionar errores aleatorios y permite compararlos con el valor real, lo que facilita la detección de cualquier error sistemático.

También ayuda a evaluar la reproducibilidad y la repetibilidad, que son aspectos esenciales del método científico. Además, Excel puede medir la variabilidad estadística entre los puntos de datos y garantizar la precisión de la resolución de las mediciones. Ayuda a identificar cualquier sesgo potencial, que puede ser intrínseco al conjunto de datos, mejorando así la calidad general de los datos.

Google Analytics para mediciones precisas y exactas.

Google Analytics permite realizar mediciones precisas al proporcionar una gran cantidad de puntos de datos para analizar. Aprovechando el error de observación y la variabilidad estadística, la herramienta ayuda a determinar el valor real y a comprender los errores sistemáticos recurrentes. Al iterar el método científico de hipótesis, experimentación y análisis dentro de los datos numéricos, se promueve la repetibilidad y la reproducibilidad.

El método ayuda a reducir los sesgos y los errores aleatorios gracias a sus funciones que los corrigen automáticamente, lo que da lugar a una resolución de medición más precisa. Sin embargo, hay que tener cuidado con la variabilidad inherente a cualquier muestra estadística, que puede distorsionar los resultados deseados.

Mejorar la exactitud y precisión en la recopilación de datos.

Mejorar la exactitud y la precisión en la recopilación de datos son objetivos clave del método científico. Minimizar los errores de observación, los errores sistemáticos y los errores aleatorios puede dar lugar a datos más cercanos al valor real. Lograr una mayor resolución de medición también puede refinar los puntos de datos recopilados.

Técnicas como aumentar el tamaño de la muestra estadística y mejorar la repetibilidad y reproducibilidad de los experimentos pueden ayudar a reducir la variabilidad estadística. Además, un análisis numérico adecuado puede abordar el sesgo, mejorar la precisión y controlar la variabilidad de los datos recopilados.

Para que un estudio sea fiable y creíble, es fundamental lograr un equilibrio entre alta exactitud y alta precisión, ya que esto repercute en la calidad general de los datos y en las conclusiones posteriores.

Mejores prácticas para mejorar la precisión

Para mejorar la precisión en cualquier proceso científico, tenga en cuenta estos consejos. Minimizar el error de observación y el error sistemático siguiendo rigurosamente el método científico y manteniendo la coherencia en las técnicas de medición. Aumenta la resolución de medición, lo que permite capturar puntos de datos más precisos. Esto mejora la reproducibilidad y la repetibilidad, y reduce el sesgo.

Las mediciones frecuentes también pueden reducir los errores aleatorios y garantizar que el valor real se encuentre dentro del rango de variabilidad estadística. Además, ampliar la muestra estadística facilita el análisis numérico y reduce la variabilidad.

Por último, confirme siempre las observaciones para validar los resultados, promoviendo la precisión y la fiabilidad.

Mejores prácticas para mejorar la precisión

Para mejorar la precisión en los experimentos científicos es necesario utilizar con diligencia el método científico y prestar mucha atención a los detalles. Una de las mejores prácticas consiste en reducir el error de observación mediante la resolución de medición, mejorando la calidad de los puntos de datos capturados. Esto puede incluir el uso de instrumentos precisos, la realización de múltiples mediciones y el cálculo del promedio del resultado para combatir los errores aleatorios y la variabilidad estadística.

Otra práctica fundamental es aumentar la reproducibilidad y repetibilidad de los experimentos, garantizando que los resultados sean consistentes en múltiples ensayos. Por último, la reducción del sesgo y el error sistemático puede lograrse mediante una muestra estadística representativa, lo que permite acercar los resultados al valor real.

Ejemplos prácticos de exactitud frente a precisión en situaciones reales

Cuando hablamos de «precisión» en ciencia, nos referimos a cuán cerca está una medición de la realidad. ¿Precisión? Todo depende de cuántas veces puedas obtener ese mismo resultado una y otra vez. Tomemos como ejemplo una balanza. Si sigue indicando que algo pesa 10,5 libras cuando en realidad pesa 10, se trata de un error que se repite constantemente. La báscula marca medio kilo menos cada vez.

Ahora, imagina una báscula que no se decide y muestra cualquier valor entre 9 y 11 libras para un objeto que pesa 10 libras. Este tipo de lectura desordenada apunta a errores aleatorios. No es exacto, pero podría ser más preciso en promedio. Así es como utilizamos los números para averiguar qué está fallando, como los sesgos o si nuestras herramientas no son lo suficientemente precisas.

Exactitud frente a precisión en las campañas de marketing

Hablemos de marketing. Hacer las cosas bien, o «precisión», se refiere a cuán cerca están los resultados de la prueba de lo que realmente es cierto. Se ve afectado por factores como el sesgo o la simple aleatoriedad. Luego está la «precisión», que consiste en obtener los mismos resultados cada vez que se intenta. Esto se ve obstaculizado por los errores que cometemos cuando vemos y grabamos cosas.

Exactitud frente a precisión en las previsiones financieras

En el mundo del dinero, acertar, o «preciso», se refiere a lo cerca que están tus predicciones de lo que realmente va a suceder. Se trata de evitar sesgos y errores, ya sean aleatorios o simplemente porque algo no encaja. La precisión es un poco diferente. Se trata de cuán precisos son tus cálculos sobre lo que crees que va a suceder. Se trata de ser constante, incluso cuando hay un montón de cosas que podrían desanimarte.

Conclusión: equilibrio entre exactitud y precisión para obtener resultados óptimos.

Para dominar cualquier método científico, es fundamental encontrar un equilibrio entre exactitud y precisión. Ambos aspectos ayudan a reducir el error de observación y a lograr una aproximación más cercana al valor real. Las mediciones precisas, con menos errores sistemáticos, mejoran la fiabilidad de la extracción de muestras estadísticas, lo que aumenta la reproducibilidad.